Gerçel sayilar (veya Reel sayilar), Rasyonel sayilar kümesinin standart metrige göre bütünlenmesiyle elde edilen kümedir. Reel sayilar kümesisembolüyle gösterilir.
Basit aritmetik teknikleriyle kolayca ispatlanabilecegi üzere, tüm rasyonel sayilarin tekrar eden birer ondalik açilimi vardir. Mesela
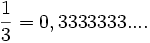
veya
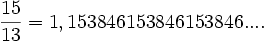
esitliklerinde oldugu gibi. Burada dikkat edilmesi gereken, ondalik basamaklardaki rakamlarin bir süre sonra bloklar halinde periyodik tekrar etme özelligidir. Rasyonel sayilardan reel sayilari elde etme islemini ise rasyonel sayilara ondalik açilimindaki rakamlarin periyodik tekrar etmedigi sayilarin eklenmesi olarak düsünülebilir. Bu tür sonradan elde ettigimiz reel sayilara irrasyonel sayilar denir.
Irrasyonel Sayilara Örnekler
Bazi Yan Bilgiler:
- Tam kare olmayan hiçbir dogal sayinin karekökü rasyonel degildir.
- Rasyonel sayilar kümesi'nin sayilabilir olmasina karsilik Reel sayilar kümesi sayilamazdir.
- Irrasyonel sayilar da kendi içlerinde "cebirsel sayilar" ve "askin sayilar" olarak ikiye ayrilirlar.
- Irrasyonel sayilarin varliginin ilk Yunan matematikçi Pisagor tarafindan anlasilmis oldugu görüsü yaygindir. Fakat Pisagor bu sayilarin evrenin düzenine aykiri oldugunu düsünmüs ve ögrencilerine bu sayilarin varligini açiklamayi yasaklamistir.
- Arsimet Özelligi: x ve y birer reel sayi olsun ve x sifirdan büyük olsun. Bu durumdanx > y özelligini saglayan bir n dogal sayisi vardir.
__________________









 Alıntı
Alıntı